As the CEO of Growth Science, Thomas Thurston comments: “I think of data science as a way of thinking about the world in terms of hypotheses, testing, confidence, and error margins.” Machine learning involves selecting algorithms, sampling data, setting parameters to optimize accuracy of learning accuracy. How to get the most fruitful results means that you need to action right at the earliest stage. Here I will cover the relationship among bias, variance, regulation parameters, and number of sample data.
More data means better results?
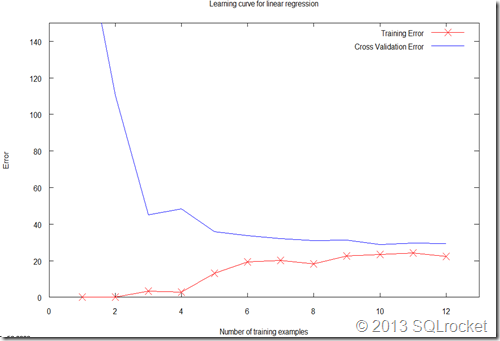
It is not always the case. As the learning curve shown below, when we increase the number of training samples, both training error and cross validation error are still very large. A learning curve plots training and cross validation error as a function of training set size.
Here we split a dataset into training, validation and test sets to be 60% training set, 20% validation set, and 20% test set as typical practices do. The learning algorithm finds parameters {theta} to minimize training set error and use these parameters {theta} to estimate errors on cross validation dataset and test set.
Best practice for high bias
The poor performance on both the training and test sets suggests a high bias problem. Sometimes it is also called “underfitting the training data”, meaning that the learning model has not captured the information in the training set. Thus, adding more data won’t help. In order to improve both training and test set performance, here are actions to take:
- Adding more complex features (also known as degrees of freedom) to increase the complexity of the hypothesis.
- Increase the degree d of the polynomial. This allows the hypothesis to fit the data more closely, improving both training and test set performance.
- Decreasing the regularization parameter lambda to allow the hypothesis to fit the data more closely.
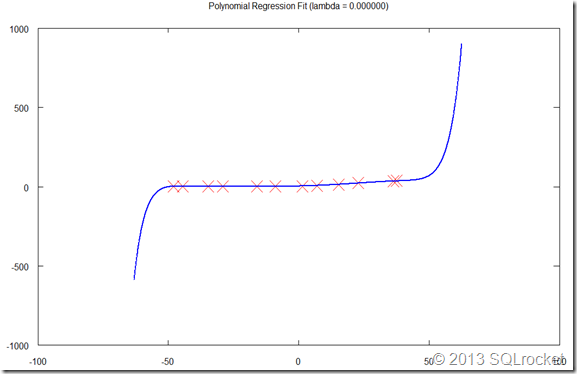
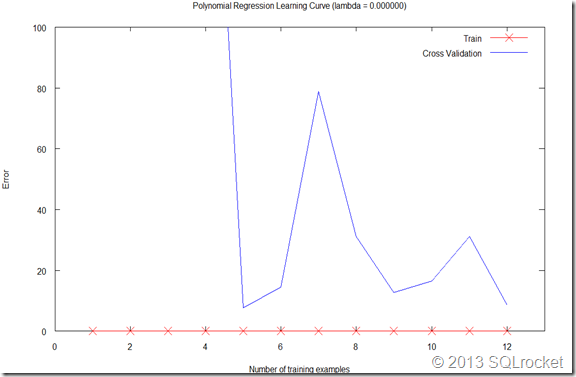
Figure 2 demonstrates that when we increase the degree of polynomial in regression, the model fits training data better and the error for training sets is almost zero. However, the cross validation error are still very large. Also, you may notice the big jump at the two ends of fitting curve. This comes from the nature of high degree of polynomials. It is the sign of high variance.
Best Practice for High Variance
High variance means the learning model is overfitting the training data. One sign of overfitting is the gap in errors between training and test. Here are the actions that can be taken to help:
- Use fewer features or decrease the degree d of the polynomial. Using a feature selection technique may be useful, and decrease the over-fitting of the estimator.
- Adding more training data to reduce the effect of over-fitting.
- Increase Regularization. Regularization is designed to prevent over-fitting. In a high-variance model, increasing regularization properly can lead to better results.
Bias-variance Tradeoff
So as you can see, to find a model with the balance of bias and variance is one of the most important goals in machine learning. As Stanford Professor Andrew Ng suggested in his Machine Learning course:
In practice, especially for small training sets, when you plot learning curves
to debug your algorithms, it is often helpful to average across multiple sets
of randomly selected examples to determine the training error and cross
validation error.
In other words, here are the main two steps:
- Learn parameters {theta} using the randomly chosen training set.
- Evaluate the parameters and choose the optimal regulation parameters lambda using cross validation dataset.
After that, evaluation training and cross validation error by trying out the following ways to find the bias-variance tradeoff:
- Get more training examples
- Reduce of increase the number of features or degree of freedom
- decrease or increase regulation parameters lambda